3 aporia - nghịch lý nổi tiếng thời kỳ cổ đại của nhà triết học Zenon. Đó là những nghịch lý sai lầm. Vậy bạn chứng minh được Zenon đang ngụy biện? Hãy thử sức bạn nhé!
1. Nghịch lý Achilles và con rùa

Trong một cuộc chạy đua, người chạy nhanh nhất không bao giờ có thể bắt kịp được kẻ chậm nhất. Kể từ khi xuất phát, người đuổi theo trước hết phải đến được điểm mà kẻ bị đuổi bắt đầu chạy. Do đó, kẻ chạy chậm hơn luôn dẫn đầu.
Trong nghịch lý Achilles và rùa, Achilles chạy đua với rùa. Ví dụ Achilles chấp rùa một đoạn 100 mét. Nếu chúng ta giả sử rằng mỗi tay đua đều bắt đầu chạy với một tốc độ không đổi (Achilles chạy rất nhanh và rùa rất chậm), thì sau một thời gian hữu hạn, Achilles sẽ chạy được 100 mét, tức anh ta đã đến được điểm xuất phát của con rùa. Nhưng trong thời gian này, con rùa cũng đã chạy được một quãng đường ngắn, ví dụ 10 mét. Sau đó Achilles lại tốn một khoảng thời gian nữa để chạy đến điểm cách 10 mét ấy, mà trong thời gian đó thì con rùa lại tiến xa hơn một chút nữa, và cứ như thế mãi. Vì vậy, bất cứ khi nào Achilles đến một vị trí mà con rùa đã đến, thì con rùa lại cách đó một đoạn. Bởi vì số lượng các điểm Achilles phải đến được mà con rùa đã đi qua là vô hạn, do đó anh ta không bao giờ có thể bắt kịp được con rùa.
Nhưng trong thực tế, người chạy nhanh hơn có thế vượt lên trước con rùa! Bạn sẽ lập luận thế nào để chứng minh nghịch lý đó của Zenon là ngụy biện?
2. Nghịch lý phân đôi hay nghịch lý đường đua

Một chuyển động phải đến được vị trí nửa quãng đường trước khi đến được đích.
Giả sử Homer muốn bắt một chiếc xe buýt đang dừng ở đó. Trước khi ông đến được vị trí chiếc xe buýt thì ông phải đến được trung điểm của khoảng cách giữa ông và chiếc xe buýt. Mà trước khi ông đến được trung điểm ấy, thì ông phải đến được điểm 1/4 khoảng cách. Mà trước khi đến được điểm 1/4 ấy ông phải đến được điểm 1/8. Trước điểm 1/8 là 1/16. Và cứ thế cho đến muôn đời. Điều đó có nghĩa rằng một vật muốn chuyện động tới địch phải vượt qua vô số trung điểm. Điều đó là không thể. Do đó vật chuyển động sẽ không bao giờ tới đích được.
Nhưng trong thực tế, vật chuyển động, giả sử không có gì ngăn cản, nó có thể đi tới đích. Điều đó chứng minh nghịch lý của zenon chỉ là ngụy biện. Vậy, nếu là bạn, bạn sẽ lập luận thế nào để chứng minh điều ấy?
3. Nghịch lý mũi tên bay
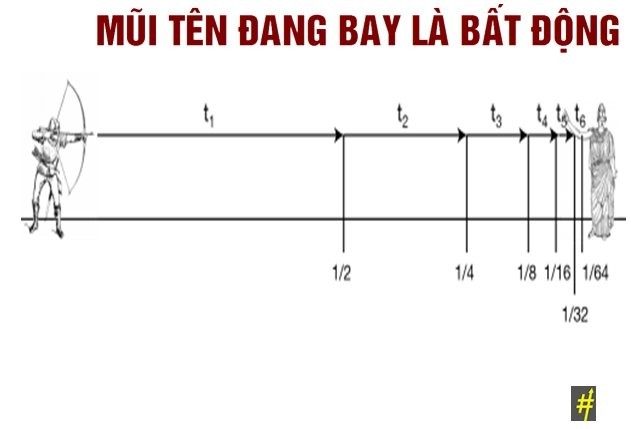
Nếu tất cả mọi thứ đều chiếm 1 khoảng không gian khi nó đứng yên, và nếu khi nó chuyển động thì nó cũng chiếm một khoảng không gian như thế tại bất cứ thời điểm nào, do đó mũi tên đang bay là bất động.
Trong nghịch lý mũi tên, Zeno nói rõ rằng để chuyển động xảy ra, thì đối tượng phải thay đổi vị trí mà nó chiếm giữ. Ông đã đưa ra ví dụ về một mũi tên đang bay. Ông lập luận rằng trong bất kỳ một khoảnh khắc (thời điểm) nào đó thì mũi tên không di chuyển đến vùng không gian nó đang chiếm, và cũng không di chuyển đến vùng không gian mà nó không chiếm. Nó không thể đang di chuyển đến nơi mà nó không chiếm, bởi vì thời gian không trôi để nó di chuyển đến đó, nó cũng không thể đang di chuyển đến nơi nó đang chiếm, bởi vì nó đã đứng đó rồi. Nói một cách khác thì tại mỗi khoảnh khắc của thời gian, không có chuyển động xảy ra. Nếu mọi vật đều bất động trong mỗi khoảnh khắc, và thời gian hoàn toàn là bao gồm các khoảnh khắc, thì chuyển động là không thể xảy ra.
Nhưng trong thực tế, rõ ràng mũi tên đang bay là nó đang chuyển động dần tới đích. Vậy bạn sẽ lập luận thế nào để chứng minh nghịch lý này của Zenon chỉ là ngụy biện?
Trên đây là 3 aporia - nghịch lý mà nhà triết học thời kỳ cổ đại Hy Lạp sáng tạo ra. Thời nay, ai có thể chứng minh được nhà triết học này rơi vào ngụy biện.
Không có nhận xét nào:
Đăng nhận xét