Theo lẽ thường, Achilles sẽ dùng tốc độ siêu việt của mình để chạy vượt mặt con rùa, nhưng triết học lại bảo mọi chuyện không đơn giản vậy. Truyện ngụ ngôn rùa và thỏ cũng lấy cảm hứng từ đây đó nhỉ?
Gần 2.500 năm trước, triết gia lỗi lạc Zeno của Hy Lạp cổ đại viết một cuốn sách về các nghịch lý. Bản chất của nghịch lý là khó hiểu, nhưng may mắn thay, ta vẫn có “Achilles và con Rùa” thuộc hàng dễ hiểu nhất. Dưới đây là những yếu tố cơ bản mà Zeno nêu lên, dù đã được hàng thế hệ kể lại dưới nhiều dạng khác nhau nhưng vẫn còn lưu được giá trị thuở ban đầu:
Người hùng nổi tiếng của Cuộc chiến thành Troia, Achilles (chúng ta vẫn biết tới anh và "gót chân A-sin" oan nghiệt) chạy đua với một con rùa thấp kém. Ngạo nghễ, Achilles cho phép rùa chạy trước. Chặng đua không có gì khó khăn với một chiến binh dũng mạnh và nhanh nhẹn, nhưng mọi chuyện không dễ dàng thế: để chạy vượt được con rùa, anh phải bắt kịp nó trước đã.
Khi Achilles rút ngắn khoảng cách giữa mình và rùa, con vật chậm chạp lại tạo ra một khoảng cách mới. Dù khoảng cách mới nhỏ hơn khoảng cách giữa rùa và Achilles, Achilles phải chạy thêm cả khoảng cách mới để đuổi kịp được rùa.
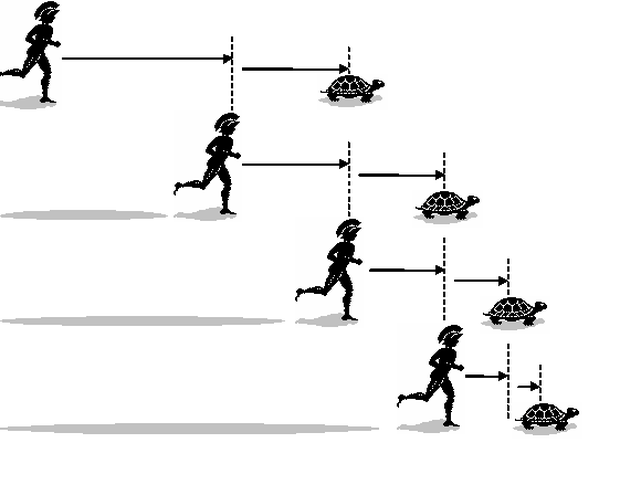
Anh tiếp tục chạy, nhưng trong khoảng thời gian đó, con rùa lại tạo ra một khoảng cách nữa rồi, ép Achilles phải chạy nốt cả khoảng cách mới nhất để đuổi kịp.
Đây là một vòng lặp vô tận, cho thấy Achilles chẳng bao giờ đuổi kịp được con rùa. Dù tốc độ chạy của Achilles có cao tới đâu, khoảng cách mới vẫn luôn xuất hiện; dù nhỏ hơn nhiều những lần trước, nhưng đây vẫn là khoảng cách cho phép con rùa luôn chạy trước Achilles.
Người đọc nghịch lý sẽ có xu hướng phủ nhận lập luận của Zeno, nhưng phản ứng đó dựa trên hai yếu tố, hoặc là lười biếng hoặc là sợ hãi.
- Lười biếng, bởi lẽ chỉ cần nghĩ tới phép nghịch lý này, ta có ngay cảm giác gần giải được rồi, nhưng thực ra chẳng bao giờ giải được. Đó cũng chính là cảm giác của Achilles khi đuổi mãi mà chẳng kịp con rùa.
- Sợ hãi, bởi lẽ ta đang bị một ông lão vượt mặt, một ông già qua đời trước cả khi con người luận ra được con số 0 thần thánh . Con người thông minh của thời hiện đại không thể kém cỏi như vậy được!
Nhưng nếu con cái bạn đọc được nghịch lý này, rồi đòi cha mẹ chúng giải thích thì sao? Bạn khó có thể cãi cùn theo kiểu “Achilles chạy nhanh hơn, rõ ràng sẽ vượt mặt con Rùa”; câu trả lời chẳng thú vị chút nào so với câu đố nghĩ ra bởi Zeno từ 2.500 năm trước. Trong chính câu đố, Zeno cũng đã ngầm bảo Achilles chạy nhanh hơn con rùa rồi: khoảng cách con rùa tạo mới luôn nhỏ hơn rất nhiều khoảng cách giữa Achilles và rùa trước đó.
Vậy ta phải nhờ tới sự giúp sức của một số nhà triết học, nhà toán học, để trả lời cho ra nhẽ. Đa số những bộ óc lỗi lạc đó cho rằng có thể viết cả sách về nghịch lý này (mà cũng có người viết rồi cơ), nhưng sau khi hỏi xin ý kiến, cây bút Brian Palmer, đưa tin cho báo Slate, đúc kết lại để chia vấn đề thành ba mục lớn như sau.
Bước một: Đây rõ là cú lừa, nhưng lừa kiểu gì nhỉ?
Zeno luận ra nghịch lý này để ủng hộ luận điểm: thay đổi và sự vận động không có thật. Nick Huggett, một triết gia ngành vật lý tại Đại học Illinois, cho rằng: luận điểm bác bỏ vật động của Zeno “quả thực điên rồ, nhưng chấp nhận nó là sự thực thì còn tệ hại hơn”.
Nghịch lý mở ra điểm mới, cho ta thấy sự lệch lạc giữa cách con người nghĩ về thế giới và bản chất của chính thế giới. Joseph Mazur, giáo sư danh dự ngành toán học tại Đại học Marlboro, mô tả nghịch lý này là “trò lừa để đánh lạc hướng suy nghĩ của bạn về không gian, thời gian và chuyển động”.
Thử thách mới xuất hiện: chính xác thì ta đã nghĩ sai ở đâu? Chuyển động hoàn toàn có thực, rõ ràng là người thì chạy nhanh hơn rùa mà? Vấn đề hóc búa nằm tại “khái niệm của loài người về vô tận ”.
Bước hai: Nhận ra là có nhiều khái niệm vô hạn khác nhau.
Thử thách đặt trước Achilles dường như bất khả thi, bởi anh sẽ phải “thực hiện vô hạn số hành động trong một khoảng thời gian hữu hạn”, nhà toán học Mazur nói, nhắc tới những khoảng cách Achilles phải chạy hết để đuổi được con rùa. Nhưng cách để tạo ra vô hạn không chỉ có một.
Trong Toán học , ta có hai chuỗi số là hội tụ và phân kỳ.
Với chuỗi phân kỳ hiển nhiên như 1+2+3+4 …, ta không có kết quả cuối cùng, hay chính xác hơn, kết quả là vô tận. Nếu như Achilles phải chạy hết những đoạn đường nhỏ liên tục được tạo ra trong suốt cuộc đua, Achilles sẽ chẳng bao giờ bắt kịp con rùa.
Nhưng giờ thử tính tới dãy số 1/2 + 1/4 + 1/8 + 1/16 …, mặc dù dãy số cũng chạy tới vô hạn, đây lại là chuỗi số hội tụ với kết quả cuối cùng là 1. Achilles cứ miệt mài chạy, liên tục biến những khoảng cách mới con rùa tạo ra ngày một nhỏ lại, người hùng thời chiến nổi tiếng sẽ đuổi kịp con rùa trong một khoảng thời gian nhất định.
Vẫn có trường hợp Achilles không đuổi được con rùa, dù cho anh chạy nhanh hơn rõ ràng. “Dựa trên Toán học mà nói, việc một vật chạy nhanh phải đuổi một vật chạy chậm tới vô tận và không bao giờ đuổi kịp là hoàn toàn khả thi”, nhà toán học Benjamin Allen nói, “chỉ cần cả hai thứ cứ tiếp tục di chuyển chậm lại theo một kiểu nhất định”.
Lại một lần nữa, bí mật của câu đố nằm tại sự kỳ diệu của toán học, cụ thể lại là chuỗi số hội tụ và phân kỳ.
Ví dụ, chuỗi 1/2 + 1/3 + 1/4 + 1/5 … trông có vẻ hội tụ, nhưng thực tế lại là chuỗi phân kỳ. Nếu Achilles chạy phần đầu của cuộc đua với vận tốc 1/2 km/h, và con rùa chạy với tốc độ 1/3 km/h, rồi chậm xuống thành cặp tốc độ 1/3 và 1/4 km/h, rồi cứ thế … thì con rùa sẽ luôn luôn chạy trước Achilles.
Bước ba: Đây không đơn thuần là giả thuyết.
Đầu óc của trẻ em non nớt nhưng khó đoán trước câu hỏi chúng có thể có lắm. Nếu như chúng đã đọc được tới bài toán khó của Zeno và ta trả lời chúng như trên, thì đứa nhóc láu lỉnh sẽ tiếp tục hỏi: tại sao ta biết tổng của 1/2 + 1/4 + 1/8 + 1/16 … là 1? Chẳng ai làm được phép tính này, bởi vì nó kéo dài tới vô hạn.
Theo một cách hiểu nhất định, kết luận về việc một dãy số vô tận có tổng là một con số hữu hạn chỉ là một giả thuyết, được luận ra và hoàn thiện bởi những bộ não vĩ đại của Isaac Newton hay Augustin-Louis Cauchy, những người tìm ra cách ứng dụng công thức toán học để khẳng định một chuỗi số là hội tụ hay phân kỳ.
Nhưng chỉ coi nó là một giả thuyết thì chưa xứng tầm.
“Rất dễ để nói lời khẳng định một chuỗi số cộng lại thành một con số hữu hạn”, nhà toán học Huggett nói, “nhưng cho tới khi bạn có thể chứng minh được - một cách chặt chẽ - cách để cộng một chuỗi số vô tận bất kỳ, thì đó chỉ là lời nói sáo rỗng. Chính Cauchy đã cho nhân loại câu trả lời”.
Chuỗi số hội tụ giải thích được vô vàn thứ hiện hữu trong thế giới hiện tại. Không chỉ cách một người chạy nhanh (như Achilles) có thể vượt mặt con rùa, mà:
Mọi khoảng cách, khoảng thời gian hay lực nào tồn tại quanh ta đều có thể bị phân tách thành một chuỗi số vô tận (cũng giống như số khoảng cách Achilles phải chạy để bắt kịp con rùa), nhưng hàng thập kỷ tính toán các khía cạnh về vật lý và kỹ thuật đã chứng minh cho ta thấy kết quả cuối cùng vẫn là một số duy nhất, một kết quả hữu hạn.
Câu trả lời trên có thể không thỏa mãn được Zeno, cũng như nhiều triết gia vẫn có lối nghĩ “logic của họ vượt tầm thực tại”. Nhưng với cái cách cộng đồng toán học và triết học trả lời câu đố của Zeno, sử dụng những quan sát đã có để áp dụng kỹ nghệ đảo ngược vào một giả thuyết đã luận được ra, chính là ví dụ rõ ràng nhất cho ta thấy tầm quan trọng của nghiên cứu và thử nghiệm trong việc mở khóa những bí mật của Vũ trụ.
Đây chính là lời phản biện cho bất cứ ai đặt dấu hỏi cho tầm quan trọng của việc nghiên cứu khoa học, triết học, toán học hay bất cứ lĩnh vực nào.



Không có nhận xét nào:
Đăng nhận xét